De verkiezingen voor het Europese Parlement zijn weer voorbij. Het waren wonderlijke verkiezingen met een partij die wel de meeste stemmen kreeg, maar niet de meeste zetels, en met een partij die wel de meeste zetels kreeg, maar niet de meeste stemmen.
En dan was het ook nog zo dat de uitslag voor Nederland pas drie dagen na het stemmen bekend werd gemaakt. Dit laatste leidde in Nederland tot bijzondere situaties. Er was een echte exit poll van Ipsos, en dan waren er ook de voorspellingen van Peil.nl en GeenStijl op basis van het bijwonen van de telling van de stemmen in een aantal stembureaus.
Kansrekening
Hoe goed waren deze voorspellingen nu eigenlijk? Goede peilingen maken gebruik van de klassieke steekproeftheorie. Die theorie schrijft voor dat je steekproeven moet loten uit de te onderzoeken populatie. Alleen dan kun je de uitkomsten van je onderzoek generaliseren naar de hele populatie. Door gebruikt te maken van zogenaamde kanssteekproeven kun je allerlei resultaten uit de kansrekening toepassen. Zo kun je aantonen dat je schattingen (bij benadering) een normale verdeling hebben. En ook kun je betrouwbaarheidsintervallen berekenen.
Zo’n interval geeft aan hoe ver schatting en werkelijke waarde uit elkaar kunnen liggen. Ook de onzekerheidsmarge is hiervan afgeleid. Die marge is gedefinieerd als de helft van de breedte van het betrouwbaarheidsinterval en geeft de maximale afwijking tussen schatting en werkelijke waarde weer. Vind je in een peiling een grote onzekerheidsmarge, dan betekent dit dus dat je schatting onnauwkeurig is. De werkelijkheid kan heel anders zijn. Voor de beoordeling van de uitkomsten van een onderzoek is het dus van belang de onzekerheidsmarges te vermelden.
Ipsos publiceerde geen onzekerheidsmarges. De organisatie zegt hierover: “Het bepalen van betrouwbaarheidsmarges rondom een uitkomst, zoals dat bij representatieve steekproeven nog wel gebeurt, is bij een exit poll een nogal academische aangelegenheid. Tenslotte gebruiken we geen aselecte steekproef van stembureaus maar juist een selecte, en we ondervragen vervolgens geen steekproef van kiezers op die bureaus maar we proberen ze allemaal te bereiken.”
Ipsos concludeert dat de exit poll heel betrouwbaar is, omdat dit in het verleden bij eerdere exit poll ook het geval was. Er wordt geen wetenschappelijke onderbouwing gegeven. Het maakt het ook lastig om iets te zeggen over de nauwkeurigheid van een toekomstige poll.
De prognoses
Laten we de voorspelling van Ipsos wat nader bekijken. Hun steekproef bestond uit ongeveer 20.000 kiezers die hun stem uitbrachten bij één van de veertig door Ipsos geselecteerde stembureaus. Die stembureaus werden niet geloot maar bewust gekozen zodat ze goed verspreid waren over het land en over stad en platteland. Aan alle kiezers in die veertig stembureaus werd gevraagd nog een keer te stemmen, maar dan met een stembiljet van Ipsos. De uitkomsten staan in de tweede kolom van tabel 1.
Achteraf kun je zeggen dat de voorspelling redelijk dicht in de buurt lag van de uiteindelijke uitslag. De grootste afwijking is te zien voor de PVV, waar Ipsos 1% te laag zat. Een steekproef van 20.000 personen is vrij groot. Als die getrokken zou zijn geweest via loting met gelijke kansen (een aselecte steekproef), dan zouden de onzekerheidsmarges erg klein zijn geweest. De marge voor het CDA zou dan 0,5% zijn geweest.
Helaas zijn de 20.000 personen van Ipsos niet afkomstig uit zo’n aselecte steekproef. Er zijn doelgericht stembureaus geselecteerd en in die stembureaus zijn alle stemmers benaderd. Door deze aanpak is het onduidelijk hoe groot de kans is om in de steekproef te komen. En dus kunnen geen onzekerheidsmarges worden uitgerekend. Uiteraard kun je achteraf, nadat de werkelijke uitslag bekend is, wel controleren hoe goed of slecht de voorspellingen waren. Maar dat is mosterd na de maaltijd. Die informatie kan hooguit helpen om een toekomstige peiling te verbeteren. Waar het om gaat is dat je meteen bij het publiceren van je voorspelling ook kunt aangeven hoe goed die voorspelling is.
Clusters
De aanpak van Ipsos lijkt nog het meeste op wat in de steekproeftheorie een clustersteekproef wordt genoemd. Daarbij loot je eerst een aantal clusters, en vervolgens benader je iedereen in de geselecteerde clusters. Bij Ipsos zijn de stembureaus de clusters. Als je de clusters echt loot, dan kun je onzekerheidsmarges uitrekenen.
Het is interessant om eens uit te zoeken wat er zou gebeuren met de voorspellingen van Ipsos als je veertig stembureaus echt loot uit de verzameling van alle ongeveer 10.000 stembureaus. Daar zou wel eens uit kunnen komen dat de marges toch vrij groot zijn. Dat is een nare eigenschap van veel clustersteekproeven. Vaak lijken mensen in een cluster veel op elkaar, dus dan heeft het niet zo’n zin om veel mensen in een cluster te benaderen. Je zou ook hebben kunnen volstaan met een (aselecte) steekproef van mensen uit het stembureau. Een dergelijke steekproef wordt een tweetrapssteekproef genoemd.
Voor de nauwkeurigheid van de voorspellingen is het beter om veel clusters met weinig personen per cluster te hebben dan weinig clusters met veel personen per cluster. Aan dat eerste (veel clusters) hangt echter wel een prijskaartje.
Aselecte steekproef
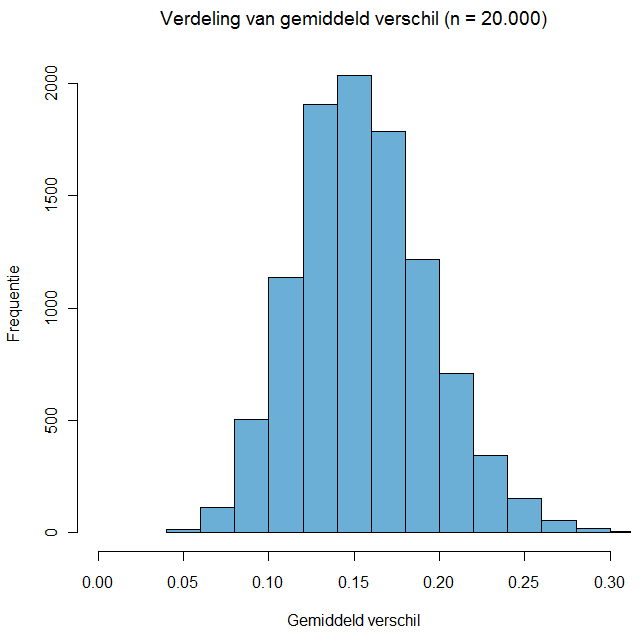
Om de voorspelling van Ipsos op waarde te kunnen schatten, is de gemiddelde absolute fout berekend. Deze gemiddelde afwijking per partij is voor Ipsos gelijk aan 0,49. Er is dus gemiddeld per partij een afwijking van ongeveer een half procent. Is dit nu een afwijking die je kunt verwachten als je een nette aselecte steekproef van 20.000 kiezers trekt? Daar kunnen we achter komen door dit proces te simuleren. Daarvoor is 10.000 keer een steekproef getrokken uit een populatie waarin de verdeling over de partijen is zoals in de laatste kolom van de tabel (de uitslag). Voor elk van de getrokken steekproeven is het gemiddelde verschil berekend. De verdeling van al die verschillen staat hieronder weergegeven.
Uit de figuur kun je aflezen dat een verschil van tussen de 0,1 en 0,2 procent heel goed kan voorkomen, maar een verschil groter dan 0,3 is wel heel erg onwaarschijnlijk. Bij Ipsos is het verschil 0,49.
Deze analyse laat zien dat het bij een andere onderzoeksaanpak mogelijk is om nauwkeuriger cijfers te krijgen. Bovendien rust de aanpak zwaar op de veronderstelling dat de stemmers in de veertig doelbewust geselecteerde stembureaus in alle opzichten representatief zijn voor alle stemmers in Nederland. Dit hoeft een volgende keer niet het geval te zijn. Dit maakt het lastig om voor een exit poll onzekerheidsmarges aan te geven.
Stembureaus
We kunnen een zelfde analyse uitvoeren voor de voorspelling van Peil.nl. De steekproef bestaat uit twee componenten: de uitslagen van 150 stembureaus met daaraan toegevoegd een online-peiling onder 10.000 mensen. Dat levert samen een steekproef op van naar schatting 85.000 personen. De stembureaus zijn niet aselect getrokken, maar geselecteerd via zelfselectie door mensen die zich spontaan gemeld hebben om het tellen van de stemmen bij te wonen. De peiling is afkomstig uit een zelfselectiepanel van Peil.nl. Bij een aselecte steekproef van omvang 85.000 kan het gemiddelde verschil hooguit 0,11 procent zijn. Bij de voorspelling van Peil.nl is het verschil echter 0,47, dus ook hier moeten we tot de conclusie komen dat er flinke afwijkingen in de steekproef zitten.
Bij steekproeven op basis van zelfselectie is de kans levensgroot dat er een vertekening in de uitkomsten zit. Die kun je proberen weg te werken (of te verminderen) door een weging uit te voeren. Daarbij ken je gewichten toe aan de deelnemers aan de peiling. Dat doe je zo dat personen in ondervertegenwoordigde groepen een gewicht groter dan 1 krijgen en personen in oververtegenwoordigde groepen een gewicht kleiner dan 1. Daarvoor heb je hulpvariabelen nodig. Voorbeelden zijn geslacht, leeftijd en opleidingsniveau. Als je bijvoorbeeld ziet dat er te weinig laagopgeleiden in je peiling zitten, dan moeten die een groter gewicht krijgen. Je maakt als het ware de respons representatief met betrekking tot opleidingsniveau.
Het deel van de respons dat bij peil.nl afkomstig is uit de onlinepeiling, kan gewogen worden, maar dat wordt lastiger voor de stembureaus. Je weet immers helemaal niets over de stemmers die langs zijn geweest in een stembureau. Daarom kun je ook geen effectieve weging uitvoeren op het niveau van individuele kiezers. Wat je eventueel wel zou kunnen doen, is het wegen van de stembureaus, waarbij je bijvoorbeeld de geografische verdeling kunt proberen representatief te maken. De vraag is echter of zo’n weging wel iets uithaalt.
#Geenpeil
GeenStijl had alleen de beschikking over uitslagen van stembureaus in de steekproef. Het waren 1287 stembureaus en dat ging in totaal om maar liefst 664.316 personen. Ook hier was er geen sprake van een aselecte steekproef van stembureaus. Als je de voorspelling vergelijkt met de werkelijke uitslag, wijken de percentages soms behoorlijk af. Bijvoorbeeld 2,5% voor het CDA. Dat zou bij zo’n grote steekproef niet moeten voorkomen als deze aselect zou zijn getrokken.
Als we aselecte steekproeven van omvang 664.316 personen simuleren uit de populatie, dan blijkt dat het gemiddelde verschil door de enorme omvang van de steekproef hooguit 0,04 procent kan zijn. Helaas is het gemiddelde verschil van de voorspelling van GeenStijl gelijk aan 0,82 procent. Alweer moeten we concluderen dat de verschillen tussen de steekproef en de werkelijke uitslag groter zijn dan nodig is voor een aselecte steekproef. Jammer, want met zo’n enorme steekproef zou je toch een heel hoge precisie moeten kunnen bereiken.
Overigens kun je ook met de gegevens van GeenStijl onmogelijk een weging van de deelnemers uitvoeren. Wel kunnen de stembureaus worden gewogen om de verdeling over het land representatief te maken. Volgens de informatie van GeenStijl is er wel een weging uitgevoerd. Het is echter niet duidelijk wat voor weging dat was, en of die weging ook effectief was.
Steekproefgrootte
Het is goed nog eens te benadrukken dat het publiceren van voorspellingen zoals in tabel 1 alleen zin hebben als er ook een of andere aanduiding van de onzekerheidsmarges is. Daarvoor is het belangrijk om steekproeven zoveel mogelijk te loten. Dat maakt een onderzoek misschien wel duurder, maar het is de prijs die je moet betalen voor goede cijfers. Overigens heeft GeenStijl wel een foutmarge gepubliceerd (1,5%), maar het is mij niet duidelijk hoe die is berekend, wanneer die is berekend en hoe die moet worden geïnterpreteerd. Enige transparantie zou hier nuttig geweest zijn.
Tenslotte is het goed om nog even op te merken dat een grote steekproef niet helpt om de door een bepaalde onderzoeksaanpak veroorzaakte vertekening weg te werken. Sterker nog: de grootte van de vertekening is onafhankelijk van de omvang van de steekproef. De meer dan 600.000 personen in het onderzoek van GeenStijl bieden dus geen enkele garantie dat er geen vertekening zal optreden.


Een aardige analyse die de beperkingen (maar toch ook de kracht) van dit soort onderzoeken nog eens op een rij zet.
De conclusie dat een simpele aselecte steekproef kleinere foutmarges geeft dan een geclusterde steekproef, zeker als dat cluster niet aselect geselecteerd is (vooral als er sprake is van ‘zelfselectie’), is niet heel verbazingwekkend. Dat toch voor een aanpak met clusters wordt gekozen is desalniettemin begrijpelijk, zoals je zelf schrijft door het prijskaartje van een random steekproef in deze onderzoekssituatie. Je kunt moeilijk bij 2000 stembureaus 5 personen ondervragen.
Ik vond het wat merkwaardig dat Ipsos dit keer geen foutmarge aangaf, terwijl ze dat vorige keren wel deden. Toen spraken ze, als ik me goed herinner, over een simulatietechniek. Je kunt immers meerdere selecties van 40 stembureaus maken die allemaal redelijk representatief zijn. Als je die procedure op basis van volledige, bekende uitslagen vaak simuleert, zou je een indruk moeten krijgen van de onzekerheid van dit soort schattingen. Misschien geen perfecte maat, maar al een veel betere indicatie dan dat exit polls ‘heel betrouwbaar’ zijn.
Bedankt voor je opmerkingen. Het is inderdaad niet haalbaar om in 2000 stembureaus 5 personen te ondervragen. Dat zou de gegevensverzameling wel heel duur maken. Je kunt echt denken aan een tussenvorm: een ‘steekproef in ruimte en tijd’. Daarbij gaan de interviewers op aselecte gekozen uren naar aselect gekozen stembureaus. Een interviewer bezoekt dan verdeeld over de dag verschillende stembureaus in plaats van de hele dag in één stembureau blijven.